Tutorial 8: The t-distribution

The t distribution and its use in statistical hypothesis testing

Week of October 28, 2024 (8th week of classes)

How the tutorials work

The DEADLINE for your report is always at the end of the tutorial.

The INSTRUCTIONS for this report is found at the end of the tutorial.

While students may eventually be able to complete their reports independently, we strongly recommend attending the synchronous lab/tutorial sessions. Please note that your TA is not responsible for providing assistance with lab reports outside of these scheduled sessions.

The REPORT INSTRUCTIONS (what you need to do to get the marks for this report) is found at the end of this tutorial.

Your TAs

Section 0101 (Tuesday): 13:15-16:00 - Aliénor Stahl (a.stahl67@gmail.com)
Section 0103 (Thursday): 13:15-16:00 - Alexandra Engler (alexandra.engler@hotmail.fr)

General Information

Please read all the text; don’t skip anything. Tutorials are based on R exercises that are intended to make you practice running statistical analyses and interpret statistical analyses and results.

Note: At this point you are probably noticing that R is becoming easier to use. Try to remember to:

set the working directory
create a RStudio file
enter commands as you work through the tutorial
save the file (from time to time to avoid loosing it) and
run the commands in the file to make sure they work.
if you want to comment the code, make sure to start text with: # e.g., # this code is to calculate…

General setup for the tutorial
An effective way to follow along is to have the tutorial open in your WebBook alongside RStudio.

A computational approach to exploring the conceptual development of the t-distribution over a century ago.

Let’s assume a normally distributed statistical population: mean (μ) = 98.6 and standard deviation (σ) = 5.

In this tutorial, we will construct the sampling distribution of means for this population using finite sampling. In other words, we will employ a computational approach, as in previous tutorials, to approximate the sampling distribution by:

a) generating a large number of samples from the population, b) calculating the mean and standard deviation for the sample means, and
c) building the frequency distribution of the standardized sample means (i.e., the sampling distribution of standardized values).

The sampling distribution of standardized sample means follows a t-distribution. Using this distribution, we can calculate the p-value for an observed t-value by determining the proportion of values in the t-distribution that are either greater than or equal to the observed t-value or less than or equal to its negative counterpart (-observed). The process can be summarized as follows, as discussed in class:

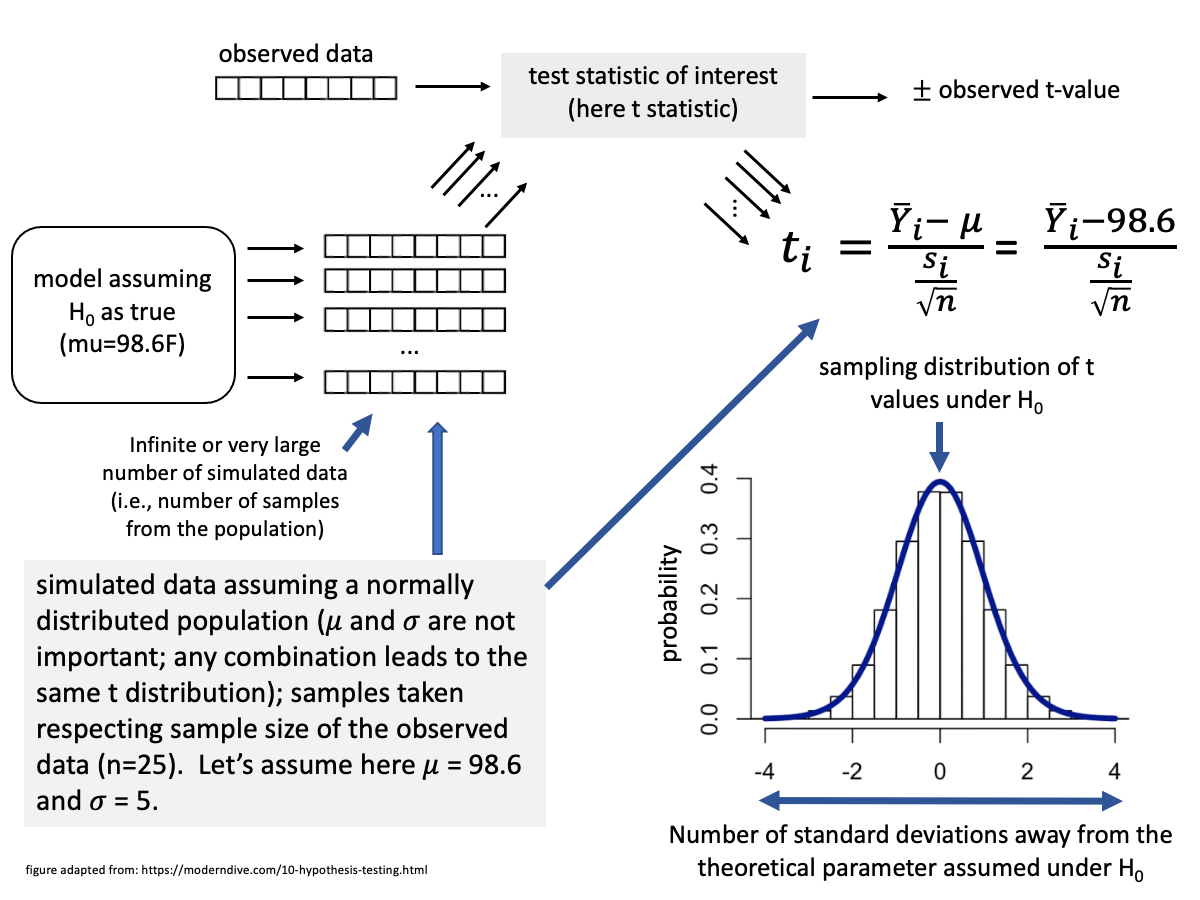
The t-distribution was originally derived through calculus under the assumption of infinite sampling. However, a finite approximation using computational methods helps us grasp the intuition behind its construction. In this example, the t-distribution will be approximated using a sample size (n) of 25 observations (i.e., the number of individuals whose temperatures were measured). Please be patient—it will take a little time (probably just over a minute!). We will use 1,000,000 replicates for better precision, as this provides a much closer approximation of the t-distribution compared to our usual 100,000 replicates. Greater sample size is needed to achieve the necessary accuracy. Keep in mind that the actual t-distribution was derived mathematically to model the distribution under conditions of infinite sampling.

number.samples <- 1000000
samples.pop.1 <- replicate(number.samples,rnorm(n=25,mean=98.6,sd=5))
dim(samples.pop.1)

Calculate the mean and standard deviation of the sampling distribution (this will also take a little bit of time given the large number of samples):

sampleMeans.Pop1 <- apply(samples.pop.1,MARGIN=2,FUN=mean)
sampleSDs.Pop1 <- apply(samples.pop.1,MARGIN=2,FUN=sd)

As you know by now, the mean of the sampling distribution of means approximates the population mean (μ=98.6). Although they are not exactly identical due to finite sampling, both the computational and analytical (calculus-based) approaches are grounded in the same principle—constructing the sampling distribution for the theoretical population of interest, as defined under the null hypothesis.

c(mean(sampleMeans.Pop1),98.6)

Next, we calculate the standard deviation of the sampling distribution of means as sd(sampleMeans.Pop1), which is called standard error of the mean; this quantity (standard error) is equal to the standard deviation of the population (sigma = 5) divided by the square root of the sample size (n=25). Note that they are very close as well:

c(sd(sampleMeans.Pop1),5/sqrt(25))

To make the t-distribution universal, we need to standardize it. This standardization allows the t-distribution to be applicable to any continuous variable, regardless of changes in the population mean, standard deviation, or measurement units (e.g., cm, kg). The process begins by subtracting the mean of the sampling distribution of means (i.e., the population mean) from each sample mean. As a result, the transformed sampling distribution now has a mean of zero. Next, we divide these centered values by their respective sample standard errors. This two-step process—subtraction followed by division—is performed as follows:

standardized.SampDist.Pop1 <- (sampleMeans.Pop1-98.6)/(sampleSDs.Pop1/sqrt(25))

We could have also standardized by the mean of sample means since they are pretty much the same, i.e., the population mean equals the mean of all sample means:

standardized.SampDist.Pop1 <- (sampleMeans.Pop1-mean(sampleMeans.Pop1))/(sampleSDs.Pop1/sqrt(25))

Let’s calculate the mean and standard deviations of these standardized sampling distribution of means:

c(mean(standardized.SampDist.Pop1),sd(standardized.SampDist.Pop1))

As you can see, the mean for the standardized sampling distribution is very similar to zero but we would have needed in about 1000000000 to become make it literally zero; but this would had taken too long in regular laptops.

The standard deviation should closely match \(\sqrt{\frac{v}{v - 2}}\) or \(\sqrt{\frac{df}{df - 2}}\), where \(df\) represents the degrees of freedom. In this case, \(df = 25 - 1 = 24\):

sqrt(24/(24-2))

Notice how closely the value above matches sd(standardized.SampDist.Pop1). The standard deviation of the standardized t-distribution varies with the sample size (i.e., degrees of freedom) but not with the mean, which, as we observed earlier, is always zero. However, the standard deviation of the standardized t-distribution consistently equals \(\sqrt{\frac{df}{df - 2}}\), regardless of the standard deviation of the original normal distribution used to generate it. This consistency arises from the standardization process, which ensures the standard deviation is always \(\sqrt{\frac{df}{df - 2}}\).

Let’s verify the above:

number.samples <- 1000000
samples.pop.2 <- replicate(number.samples,rnorm(n=25,mean=98.6,sd=8.5)) # instead of 5 as used earlier
sampleMeans.Pop2 <- apply(samples.pop.2,MARGIN=2,FUN=mean)
sampleSDs.Pop2 <- apply(samples.pop.2,MARGIN=2,FUN=sd)
standardized.SampDist.Pop2 <- (sampleMeans.Pop2-98.6)/(sampleSDs.Pop2/sqrt(25))
c(sd(standardized.SampDist.Pop2),sqrt(24/(24-2)))

See! Even though we changed the normal population used to generate the standardized t-distribution (i.e., instead of a standard deviation of 5 as in population 1, we used a standard deviation of 8.5), the standard deviation of the standardized t-distribution remains \(\sqrt{\frac{df}{df - 2}}\).

Let’s plot the sampling distribution (zoom in so you can see it clearly). The argument prob = TRUE in the hist function ensures that the frequencies in the distribution are transformed into probabilities when plotting the histogram. Remember, as discussed in Lecture 13, since we are working with a continuous variable (i.e., temperature), we use probabilities instead of frequencies:

hist(standardized.SampDist.Pop1, prob = TRUE, xlab = "standardized mean values",ylab = "probability", main="",xlim=c(-4,4))

Now, let’s overlay the t-distribution on top of the histogram. We’ll plot the t-distribution with 24 degrees of freedom, since we used \(n = 25\) and lost 1 degree of freedom (\(df = n - 1\)) by using the sample standard deviation to standardize each sample in the sampling distribution.

The t-distribution is plotted using the curve function in combination with the dt function, which calculates the probability density function (pdf), as discussed in class, for the t-distribution with the appropriate sample size. Notice that our computer-generated approximation of the t-distribution closely matches the theoretical t-distribution derived using calculus for infinite sampling:

hist(standardized.SampDist.Pop1, prob=TRUE, xlab = "standardized mean values",ylab = "probability", main="",xlim=c(-4,4),ylim=c(0,0.4))
curve(dt(x,df=25-1), xlim=c(-4,4),col="darkblue", lwd=2, add=TRUE, yaxt="n")

Using the t-distribution for statistical hypothesis testing
We will use the example from class on human body temperature.

State the Hypotheses: - Null hypothesis (\(H_0\)): The mean human body temperature is 98.6°F.
- Alternative hypothesis (\(H_A\)): The true population mean is different from 98.6°F.

Our goal is to determine whether to reject or fail to reject the null hypothesis (\(H_0\)) by calculating the probability (p-value) of observing the given temperature, or a more extreme value, assuming the null hypothesis (\(H_0\))—that the population mean (\(\mu\)) is 98.6°F—is true.

We will begin by using the standard, calculus-based t-distribution to calculate the p-value for our data. Later, we will compare this with the approximation generated through computational methods.

In this example, we will compare the human body temperature in a random sample of 25 individuals with the “expected” temperature of 98.6°F taught in schools.

Download the spending data file

Now, lets upload and inspect the data:

heat <- as.matrix(read.csv("chap11e3Temperature.csv"))
mean(heat)
View(heat)

Let’s calculate the t statistic (also known as the t score or t deviate), as discussed in class. This statistic is the standardized value of our observed sample mean, making it comparable to the standardized t-distribution.

To compute the t statistic, we subtract the observed sample mean from the population mean (assumed to be true under the null hypothesis, \(H_0\)). We then divide this difference by the standard error of the sampling distribution. This mirrors the same process we used to build the t-distribution computationally.

Our goal now is to transform our sample in the same way, so that it becomes comparable to the standardized t-distribution:

t.value.temperature <- (mean(heat)-98.6)/(sd(heat)/sqrt(25))
t.value.temperature

What is the probability of obtaining a sample mean as extreme or more extreme (i.e., smaller since the sample mean is smaller than the target population) than 98.524°F given that the population mean is 98.6°F?

Remember that the mean of the t distribution (sampling distribution of standardized means) is zero and the t score for 98.524\(^o\)F (sample mean based on 25 people) is t = -0.5606452.

So the question becomes: “What is the probability of obtaining t scores as extreme or more extreme than -0.5606452 assuming that the population mean (when standardized) is truly zero (i.e., 98.6°F)? Remember, 98.524°F is t = -0.5606452 (i.e., when t standardized) AND 98.6°F (unstandardized) is zero (t standardized). This probability can be calculated using the function pt (pt stands for probability of t):

Prob.t.value.temperature <- pt(-0.5606452,df=24) 
Prob.t.value.temperature

The probability is 0.2901181. Since the goal is not to determine whether human body temperature is specifically lower than the value taught in textbooks, but rather to assess whether it differs (either lower or higher) from the textbook value, we use a two-tailed probability.

This two-tailed approach accounts for both sides of the t-distribution to evaluate whether the observed sample t-value (mean = -0.5606452) is consistent with the distribution of t-values under the null hypothesis, which has a mean of zero (equivalent to 98.6°F in the original sampling distribution before standardization).

Prob.t.value.temperature.bothSides <- 2*Prob.t.value.temperature
Prob.t.value.temperature.bothSides

This probability (p-value = 0.5802363) represents the relative amount of values equal or greater than 0.5606452 and equal or smaller than -0.5606452. This can be represented graphically as:

hist(standardized.SampDist.Pop1, prob=TRUE, xlab = "standardized mean values",ylab = "probability", main="",xlim=c(-4,4),ylim=c(0,0.4))
curve(dt(x,df=25-1), xlim=c(-4,4),col="darkblue", lwd=2, add=TRUE, yaxt="n")
abline(v=0.5606452,col="red",lwd=2)
abline(v=-0.5606452,col="red",lwd=2)

So values equal to the red vertical lines or smaller (left side) or bigger (right side) are then used to calculate the p-value which is then used as evidence for rejecting (against) the null hypothesis.

We also use the function t.test to calculate the same two-tailed probability as follows (look into the p-value (p-value = 0.5802):

t.test(heat, mu=98.6)

Interpreting the p-value under a statistical hypothesis testing framework:

The p-value helps build quantitative (statistical) evidence for or against the null hypothesis. Since the p-value is larger (and significantly larger) than the chosen significance level (we will use \(\alpha = 0.05\) here), we fail to reject the null hypothesis.

It is important to note that we are not concluding that the human body temperature taught in textbooks (98.6°F) is true. Rather, based on our sample, we simply cannot reject the hypothesis that the population mean is 98.6°F.

REMEMBER: We build evidence by rejecting the null hypothesis, but not in favor of accepting it.

Now, let’s calculate this probability using our computer-approximated t-distribution. To estimate the probability of obtaining t-scores as extreme or more extreme than -0.5606452, we divide the number of standardized values in our sampling distribution that are smaller than the observed t-score by the total number of sample means generated (i.e., 1,000,000):

Prob.t.finite <- length(which(standardized.SampDist.Pop1<= -0.5606452))/number.samples
Prob.t.finite*2

Note how the computer-based result and the theoretical case (i.e., using the calculus-based t-distribution with a p-value of 0.5802) are very similar. In my case, I obtained Prob.t.finite * 2 = 0.581096; your result will likely differ slightly from mine due to random variation in finite sampling.

If we could run the simulation an infinite number of times, the computer-generated value would match exactly with the theoretical value derived using calculus (i.e., with the pt function used above).

By now, you get the point!

Report instructions

All the information you need to solve this problem is provided in the tutorial.

The parameters used to create the statistical population for generating the standardized t-distribution were a mean of 98.6 and a standard deviation (\(\sigma\)) of 5. Now, create the t-distribution computationally, but this time use a mean significantly different from 98.6 and a standard deviation different from 5. Keep the sample size at 25 observational units.

Task
1. Write code to calculate the probability of obtaining t-scores as extreme or more extreme than -0.5606452 (under the assumption that \(H_0\) is true) using your newly created t-distribution.
2. Include code to plot the histogram of your t-distribution.

Question
Is there a significant difference between the probability generated from your newly created t-distribution and the one generated earlier (i.e., with \(\mu = 98.6\) and \(\sigma = 5\))?

Write a brief explanation of your findings, referencing both your code and the concepts learned in the tutorial.

# use as many lines as necessary,
# comments always starting with  #

Submit the RStudio file via Moodle.